Θεωρήματα Τεμνουσών Κύκλου

Details
Category: Ροές Διδασκαλίας
Published: Friday, 08 October 2021 14:04
Written by Super User
Hits: 140

Article Index

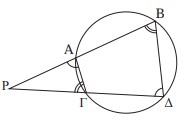
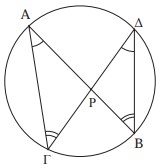
Σχήμα 17α Σχήμα 17β

Θεώρημα 1. Αν δύο χορδές ενός κύκλου ΑΒ, ΓΔ, τέμνονται σε ένα σημείο Ρ, είτε εσωτερικά, είτε εξωτερικά του κύκλου, τότε το γινόμενο  \(PA \cdot PB = P\Gamma \cdot P \Delta \) .

Προσπαθήστε να το αποδείξετε διακρίνοντας τα όμοια τρίγωνα  σε κάθε περίπτωση.

Ερώτηση: Τι συμβαίνει αν μετακινήσουμε την τέμνουσα ΡΓΔ, με Ρ εξωτερικό σημείο του κύκλου, ώστε τα Γ,Δ να ταυτιστούν, δηλαδή η ΡΓΔ να γίνει εφαπτόμενη στον κύκλο;


Αφού θυμηθείτε τον ορισμό και τα κριτήρια εγγραψιμότητας τετραπλεύρων πχ εδώ να αποδείξετε το επομενο:

Πόρισμα. Αν δύο τμήματα ΑΒ και ΓΔ ή οι προεκτάσεις τους τέμνονται σε ένα σημείο Ρ έτσι ώστε ΡΑ ∙ ΡΒ = ΡΓ ∙ ΡΔ , τότε το τετράπλευρο με κορυφές τα σημεία Α, Β, Γ, Δ είναι εγγράψιμο.

Χρυσή τομή, Ριζικός άξονας, Θεώρημα Stewart